একটি বাক্স পরিমাপ করা সহজ মনে হতে পারে, কিন্তু এর জন্যকাস্টম প্যাকেজিং, পণ্যের নিরাপত্তার জন্য এই মাত্রাগুলি অত্যন্ত গুরুত্বপূর্ণ! ভেবে দেখুন; প্যাকেজিং বাক্সের মধ্যে ন্যূনতম চলাচলের স্থান ন্যূনতম সম্ভাব্য ক্ষতির দিকে পরিচালিত করে। বাক্সের আকার যেকোনো প্যাকেজিংয়ের একটি মূল উপাদান কারণ এটি প্রয়োজনীয় উপকরণ, উৎপাদন খরচ, পরিবহন খরচ এবং আরও অনেক কিছুকে প্রভাবিত করে।
একটি বাক্সের জন্য পরিমাপ করার জন্য তিনটি প্রাথমিক মাত্রা হল দৈর্ঘ্য, প্রস্থ এবং গভীরতা। মৌলিক গণিতের মতো মনে হলেও, সতর্কতার সাথে পরিমাপের জন্য এখনও বিবেচনা এবং অপ্টিমাইজেশন প্রয়োজন। এখানে, জয়স্টার গিফট প্যাকেজিং আপনার প্রয়োজনীয় বাক্সের মাত্রা পরিমাপ করার জন্য সবচেয়ে গুরুত্বপূর্ণ বিবেচনা প্রদানের লক্ষ্য রাখে!
নিখুঁত প্যাকেজিং তৈরির প্রথম ধাপ হল একটি বাক্সের মাত্রা সঠিকভাবে পরিমাপ করার পদ্ধতি বোঝা। তাহলে, আপনার কোন মাত্রাগুলি প্রয়োজন? প্রথমে, নিম্নলিখিত মাত্রাগুলি পরিমাপ করার জন্য প্যাকেজিং বাক্সের খোলা অংশটি পরীক্ষা করুন:
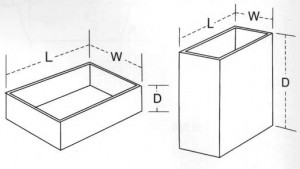
দৈর্ঘ্য (L): বাক্সের উপর থেকে দেখলে সবচেয়ে লম্বা দিক।
প্রস্থ (W): বাক্সের উপর থেকে দেখলে ছোট দিক।
গভীরতা (উচ্চতা)(D): দৈর্ঘ্য এবং প্রস্থের লম্ব দিক।
বাইরের মাত্রা নয়, ভেতরের মাত্রা পরিমাপ করুন! কেন? ধাপগুলি আরও উন্নত করার সাথে সাথে এটি আরও স্পষ্ট হয়ে উঠবে! মনে রাখবেন; যদিও তাত্ত্বিকভাবে বাক্সের উপরের এবং নীচের দিকগুলি সমান হওয়া উচিত, প্যাকেজিংয়ের ক্ষেত্রে এটি সবসময় হয় না। অতএব, আপনার প্যাকেজিং পণ্যের প্রয়োজনীয়তা পূরণ করে তা নিশ্চিত করার জন্য প্রতিটি মাত্রা সঠিকভাবে পরিমাপ করুন!
আপনার পণ্যের জন্য নিখুঁত ফিট অর্জনের জন্য অভ্যন্তরীণ এবং বাহ্যিক মাত্রার মধ্যে পার্থক্য অত্যন্ত গুরুত্বপূর্ণ। নির্মাতারা এবং আপনার পণ্যের জন্য অভ্যন্তরীণ মাত্রা আরও সঠিক! বেশিরভাগ নির্মাতারা অভ্যন্তরীণ এবং বাহ্যিক মাত্রার আকার সম্পর্কে খুব স্পষ্ট। সর্বোপরি, কেউই চায় না যে পরিমাপের ত্রুটির কারণে তাদের পণ্য ক্ষতিগ্রস্ত হোক।
যদি কোনও বাক্সের জিনিসপত্র বাইরের মাত্রার উপর ভিত্তি করে পরিমাপ করা হয়, তাহলে সেই বাক্সের জিনিসপত্রগুলি ঠিকভাবে নাও ফিট করতে পারে। এটি সম্ভাব্যভাবে নির্দিষ্ট পণ্যগুলির ক্ষতি করতে পারে যেগুলির জন্য টাইট প্যাকেজিং প্রয়োজন! সেইজন্য বাক্সের অভ্যন্তরীণ মাত্রার উপর ভিত্তি করে মাত্রা গণনা করলে যেকোনো সন্দেহ দূর হতে পারে। ঢেউতোলা বাক্সের ক্ষেত্রে এটি বিশেষভাবে গুরুত্বপূর্ণ।
আমরা আশা করি এই নিবন্ধটি আপনাকে সঠিকভাবে একটি বাক্স পরিমাপ করার পদ্ধতি বুঝতে সাহায্য করবে!
পোস্টের সময়: ডিসেম্বর-০২-২০২৩
